Traveling Salesman-problemet

Travelling salesman-problemet , som vi heretter bare kallar TSP, er ein av dei mest studerte problema i numerisk matematikk, og det fins masse testdata frå heile verda. Problemet går kort og godt ut på å finna den kortaste reiseruta gjennom eit bestemt antal byar og tilbake igjen til utgangspunktet. Kvar by skal besøkjast bare ein gong. Nedanfor er vist eksempel på problemet og ei løysing. Kan du sjå om det er den beste?

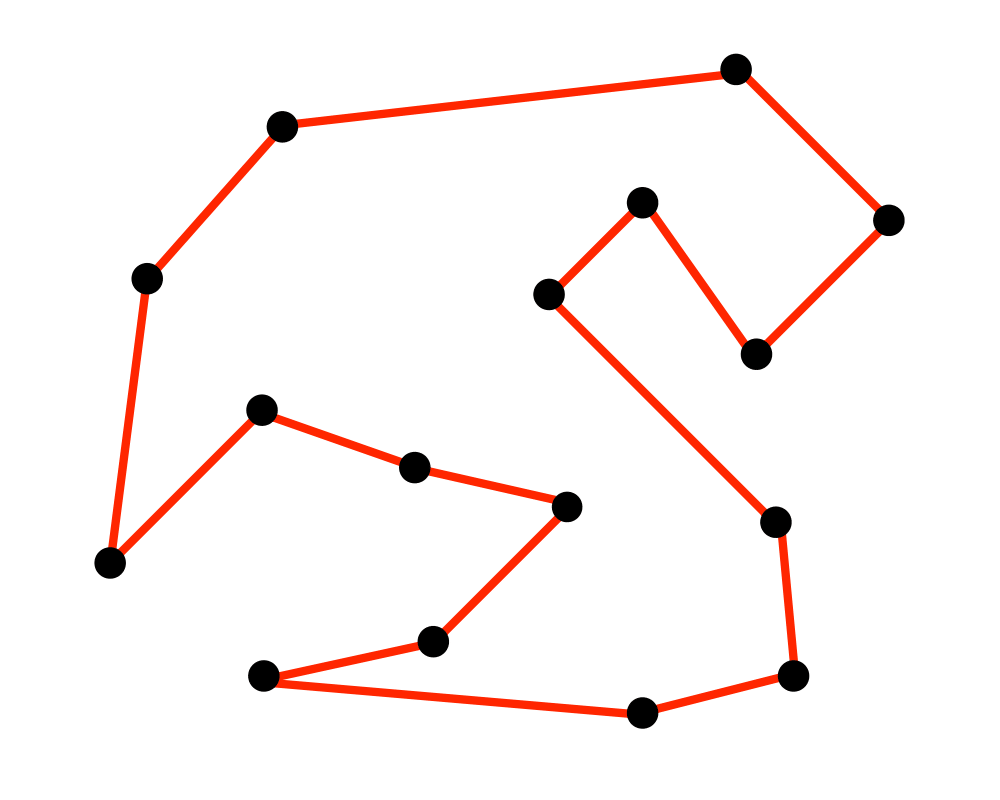
Utfordringen med TSP er at antalet løysingar eksploderer når vi aukar antalet byar. For 5 byar er det 12 unike løysingar. For 10 byar er det 181 440 unike løysingar, og for 15 byar er det over 87milliardar unike løysingar. Dette betyr at hvis vi skal prøva ut alle løysingane, så vil det ta lang tid. Hvis vi antar at det tar et mikrosekund å testa ei løysing, så viser tabellen under kor lang tid det vil ta for opp til 20 byar.

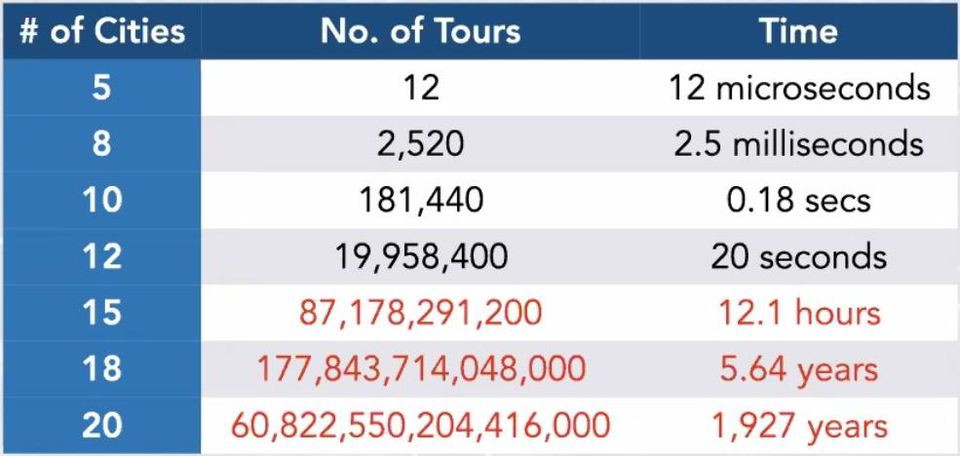
Det er to måtar å få ned tida på: enten laga raskare datamaskiner (kanskje treng vi kvantemaskiner) eller raskare algoritmar. Her skal vi sjå litt på ein del mulige algoritmar å bruka på TSP. Nedanfor er eit eksempel med sju byar. Til venstre er eit forslag til tur som allerede er ganske bra, og til høgre har vi forbedra det.

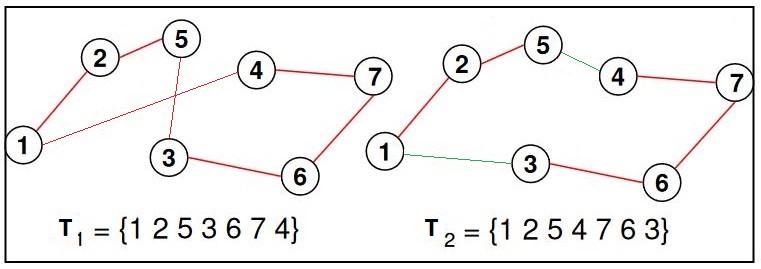
I grafteori kallast byane nodar, og veiene mellom dei for kantar. Så i dette eksempelet har vi sju nodar, og sju kantar, sidan vi jo skal tilbake til den første byen. For å rekna ut lengden av ein tur, treng du enten ein tabell som gir alle avstandane mellom kvar av byane, eller x- og y-koordinatane til punkta, slik at vi kan rekna ut avstandane. Hvis du vil gjera det meir teoretisk og dynamisk, kan du også generera tilfeldige punkt.

Den første utfordringen no er å finna ein god måte å skriva grafen vår som ein datastruktur. Sidan vi ikkje har nokon forgreiningar (som i eit tre) så er det enklaste å representera ein tur som ei tallfølge, eller rett og slett som ei (feks. Python-) liste. Turen T₁ kan derfor skrivast slik: [1, 2, 5, 3, 6, 7, 4]. Merk at den den same turen også kan skrivast med byane i motsatt rekkefølge, sidan det bare er avstanden vi er opptatt av. Vi antar med andre ord her at det er like langt frå 1 til 2 som motsatt, sjøl om det ikkje nødvendigvis er 100% korrekt i verkeligheten. Vi legg også merke til at ein syklisk permutasjon av T₁, som feks. [5, 3, 6, 7, 4, 1, 2] også er den same turen. Vi startar i by nr 5, men rekkefølgen er den same. Så for å rekna ut antalet turar, tenkjer vi oss at vi alltid startar i same by, feks. nr 1. Då har vi 6 muligheter for andre by, 5 for neste osv. Dermed skulle ein kanskje tru at antalet forskjellige turar er 6! = 720. Men når vi kombinerer på denne måten får vi samme turen to gongar. For eksempel er  turen T =[1, 2, 3, 4, 5, 6, 7] lik turen T' = [1, 7, 6, 5, 4, 3, 2]. Vi har bare tatt turen frå by 1 motsatt vei. Altså er antalet forskjellige turar lik 6!/2 = 360. For n byar er antalet (n-1)!/2. Dette gir oss fort veldig mange utrekningar å gjera, hvis vi skal sjekka alle med brute force. Med 14 byar må feks. rekna ut 13!/2 = 3113510400 variantar. Så vi vil gjerne finna ein god algoritme!

Algoritmer

Den mest intuitive algoritmen for å løysa TSP er nærmaste-nabo-algoritmen. Her går ein bare til nærmaste by for kvar gong. Naturligvis må vi utelukka byar som allerede er besøkt, og vi fortset til alle byane er besøkt, før vi vender tilbake til startbyen. Dette gir ein bra, men som regel ikkje optimal, løysing. Ein annan intuitiv metode er å begynna med knyta saman dei byane som ligg nærast kvarandre, slik at ein får mange lause fragment, som ein så kan knyta disse saman i større, slik at ein tilslutt endar med ein samanhengande graf. Også denne metoden gir bra, men ikkje nødvendigvis optimale løysingar.

Hillclimbing-agoritmen og korleis vi kan endra ein tur

Når vi går fjelltur i eit terreng som skrånar jevnt oppover, så vil kvart skritt vi tar bringa oss litt oppover. Vi ynskjer å bruka det same prinsippet her. Forskjellen er at algoritmen ikkje kjenner på forhånd om eit steg (ein endring) bringer oss nærare løysinga. Så vi må altså prøva og feila. Her er vi altså er ute etter å leita små endringar av turen som fører til at den blir kortare. Merk at dette ikkje nødvendigvis betyr ein liten endring av lista. Den minste endringen av lista vil  vera å bytta to byar. Men hvis vi ser kva det fører til på kartet, så ser vi (Bare prøv sjøl, og sjå kva som skjer!) at det faktisk fører til at fire av veiene i turen blir endra.

Eit betre alternativ (som kallast 2-opt), er å kobla om to veier. I eksempelet over viser det seg at det er lurt å endra veiene  5->3 og 4->1 slik at vi får dei nye veiene 5->4 og 3->1. Resultatet er ein kortare tur T₂. som vist på figuren. Her ser det ut til at vi har funne den beste løysinga, men i prinsippet vil ein fortsetja så lenge det er mulig å finna betre løysingar ved slike ombyttingar.

Spørsmålet er korleis vi må endra listene for å få til dette. Vi huskar at turane våre kan skrivast som  T₁ = [1, 2, 5, 3, 6, 7, 4], og T₂ =  [1, 2, 5, 4, 7, 6, 3]. Då ser vi at vi har bare reversert rekkefølgen av 4, 7, 6, 3 slik at vi får 3, 6, 7, 4. Så det å bytta om to kantar i grafen vår er det same som å reversera ein del av lista vår.

Eksempel på endring av ein tur:

La oss sjå på eit eksempel der vi kjenner den optimale turen, og at vi har nummerert byane etter den optimale rekkefølga. Det vil sei at den beste turen har lista T₁ = [1, 2, 3, .... 35]

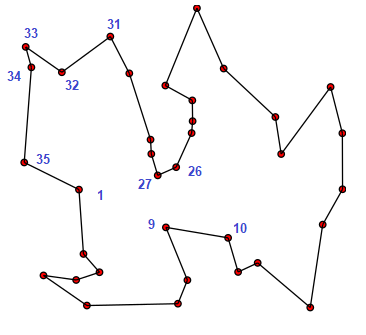
Variant 1: Knute (liten loop)

I denne turen snur vi rekkefølga på delturen 32, 33 34, og får då lista T₂ = [1, 2, 3, .... 31, 34, 33, 32, 35]. Slik ser dette ut:

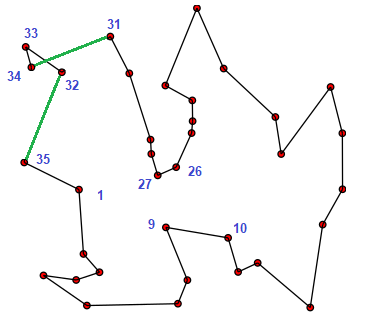
Variant 2: Kryss (stor loop):

Her snur vi rekkefølga på delturen 10, 11, ... 26. Dår får vi lista L₃ = [1, 2, 3 ... 9, 26, 25, .... 11, 10, 27, 28, .... 35]. Dette ser slik ut.

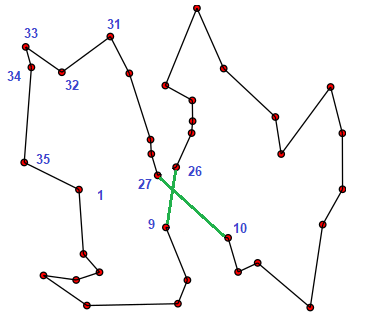
Oppsummert

Med hillclimbing startar vi med ein tilfeldig men fulstendig tur. Det betyr at vi lagar ei liste av alle byane i tilfeldig rekkefølge. Så prøver vi å gjera ein liten endring ved å reversera ein deltur. I praksis må vi då tilfeldig finna starten på del-lista og slutten, og så snu denne del-lista. Deretter reknar vi ut kor lang heile turen er, og hvis den er kortare enn den opprinnelige, så fortset vi med den nye. Så kan vi halda på med tilfeldige endringar så lenge vi har tid, eller så lenge vi ser at det skjer forbedringar. Altså har vi denne algoritmen:

1. Start med ein tilfeldig, men fullstendig tur T₁. Antagelig er dette ein veldig lang tur!
2. Finn tilfeldig ein ny tur T₂ som beskrive over.
3. Hvis T₂ er kortare enn T₁, så fortset vi med denne.
4. Gjenta frå steg 2 så lenge vi vil.

Simulated Annealing:

Begynnelsen er lik med HC, men vi innfører ein variabel kalla temperatur, som påvirker sannsynligheten for å akseptera ein lengre tur i ei gitt steg. Problemet med Hillclimbing generelt, er at den som regel set seg fast i lokale minima. Det betyr at noken gonger er det slik at det ikkje fins ein einaste endring vi kan gjera som gir ein kortare tur! Resultatet er at vi finn ei brukbar løysing, men ofte ikkje den beste. For å kunna finna den beste turen ved hjelp av slik byttingar som vi har beskrive over, så må vi av og til akseptera å gå via ein dårligare (lengre) tur. Men vi skal jo ikkje gjera det heile tida, og det er her temperaturen kjem inn. Jo høgare temperatur, jo større sannsynlighet er det for å akseptera ein lengre tur. Til å begynna med er temperaturen høg, men så blir den litt lavare for kvart steg. Algoritmen er altså slik:

1. Start med ein høg temperatur og ein tilfeldig, men fullstendig tur T₁.
2. Finn tilfeldig ein ny tur T₂.
3. Hvis T₂ er kortare enn T₁, så fortset vi med denne.
4. Hvis T₂ ikkje er kortare, kan vi likevel bytta om med ein viss sannsynlighet. Denne sannsynligheten er ein funksjon av kor mykje lenger T₂ er, og kor høg temperaturen er. Det vil sei at når temperaturen er høg, så kan det skje at vi byter til T₂, sjøl om den er ein god del dårligare. Men når temperaturen er lav, så vil vi som regel bare kunna byta til ein litt dårligare tur.
5. Gjenta frå steg 2 samtidig som vi senker temperaturen litt for kvart iterasjon.

Genetiske Algoritmer

Ein Genetisk Algoritme (GA) benytter seg av mange forslag til ruter, og denne mengda kallar vi populasjonen. For kvar ny generasjon produserer vi så nye forslag ved hjelp av krysning og mutasjon av den eksisterande populasjonen. Krysning vil sei å plukka ut to lister, og så blanda dei for å finna ein ny tur. Hvis vi bestemmer oss for å bruka same representasjon som over, så er utfordringen å konstruera ein metode som gir oss lister som representerer ein samanhengande tur. Ein tradisjonell GA vil då bare kutta dei to listene på same plass og lima i saman delene på ny. Men dette vil opplagt ikkje fungera i vårt tilfelle, for då vil vi feks. kan enda opp med same by fleire plasser i lista vår. Så vi må finna ein ny måte. Og her er mulighetene mange:

Anta at disse listene er "foreldrene". Vi plukkar ut tilfeldig ein sekvens [6, 7, 8] frå den eine lista og så set vi den inn på same plass i den andre.

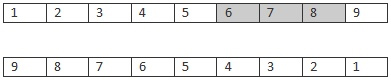
Dette fører til at sekvensen [4, 3, 2] blir fjerna frå plassane til den nye sekvensen. Spørsmålet er ka vi skal gjera med resten. Og det mest logiske, etter mi meining, er å behalda så mange som mulig på same plass i den andre forelderen. Dvs 9, 5 og 1 blir som dei er, og så bytta ut motsatt for dei andre: 4 vart fjerna og bytta med 6, så vi må setta 4 tilbake igjen. Det same kan vi gjera med 3 og 2. Denne metoden vil gi følgande liste: [9, 2, 3, 4, 5, 6, 7, 8, 1].

Men denne sida gjer det på ein litt annan måte: Dei plukkar by ("gene") for by frå forelder to frå venstre, og hvis det manglar (dvs. ikkje 6, 7 eller 8) så blir det brukt. 9 skal vera med, og blir overført til posisjon 1. Så kjem 8, 7 og 6 som blir tatt ut. Så kjem 5 som då blir putta inn i posisjon 2 fordi den er ledig. Deretter kjem 4, 3, 2 og 1. Dette gir avkom som vist under. Fordelen med denne måten er at vi har behalde sekvensen [5, 4, 3, 2] frå forelder to intakt:

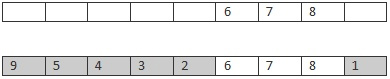
Dette er to versjonar av same tanke, nemlig å plukka ein sekvens frå den eine forelderen og fylla på med tall frå den andre. Kva som er best er ikkje greit å vita på forhånd. (Test!).

Det andre vi treng er ein mutasjonsoperator. Sida som eksempelet er teke frå, vil då bare bytta to tilfeldige byar i sekvensen. Eit klart alternativ er å bruka 2-opt som vi brukte over. Her er det også bare å testa kva som funkar best.

LENKER

Tackling the travelling salesman problem: hill-climbing. Med Python.

Traveling salesman portrait in Python. Lagar ein sti gjennom punkter i eit portrett. Bruker ein ferdig pakke.

Taveling salesman Problem. Her kan du spela interaktivt og sjå om du kan finna den kortaste veien.

Tackling the travelling salesman problem: simulated annealing. Lenke til kode.

The Traveling Salesman with Simulated Annealing, R, and Shiny. Animert + kode (som ikkje funkar!)

Applying a genetic algorithm to the traveling salesman problem.

Genetic Algorithms: The Travelling Salesman Problem.

Traveling salesman portrait in Python!
Traveling Salesman-problemet.
Stony Brook Algorithm Repository Traveling Salesman Problem.