Ein elastisk pendel er rett og slett eit lodd med masse m som er festa i ei fjør, som svingar om ein likevektstilstand. Krafta frå fjøra på loddet er (omtrent) beskriven av Hookes lov som seier at krafta er proporsjonal med utslaget x (dvs. kor langt du strekkjer den ut), men motsatt retta. Vi har altså at F = -kx. Proporsjonalitetskonstanten k kallast for fjørstivheten, og fortel kor vanskelig det er å strekkja fjøra. Jo større k, jo hardare er det. På figuren under (øverst) er fjøra strekt ut til høgre, og x er positiv. Då vil krafta F på loddet virka til venstre og er med andre ord negativ. Vi tenkjer oss her eit lodd som kan gli på eit friksjonslaust underlag. Dermed er fjørkrafta F, den einaste krafta som virkar. Du kan variera k og m i denne simuleringen for å sjå dette i praksis.
No kan vi bruka Newtons andre lov, F = ma, og vi får då likningen ma = - kx. Samtidig veit vi at akselerasjonen a er den andrederiverte av x. Dermed får vi likningen:
Dette er ein andreordens homogen differensiallikning med generell løysing x(t) = A cos(ωt + φ), der A er amplituden, dvs. det maksimale utslaget. Vi skal ikkje gå inn på løysingsmetoden (Det er R2-stoff, og du kan lesa meir om den her) Men vi kan kontrollera at løysinga passar. Då bruker vi kjerneregelen pluss at sin(x)' = cos(x) og cos(x)' = - sin(x). (Jamfør derivasjonsreglane) Hvis vi deriverer x(t) får vi v(t), og deriverer vi ein gong til, så får vi a(t):
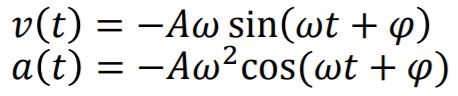
Vi ser at dette passar i difflikninga vår dersom parameteren ω er gitt ved:
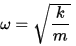
Parameteren ω fortel noko om kor fort pendelen vår svingar. Frekvensen f til eit svingesystem er antall svingningar per sekund. Og samanhengen mellom ω og frekvensen er gitt ved ω = 2πf. Dette betyr at jo stivare fjør / større k, jo hurtigare vil den svinga, og omvendt, jo større masse loddet har, jo saktare vil den svinga. Parameteren φ kallast fasen til svingningen. Hvis vi startar klokka vår akkurat når vi slepp loddet, så blir φ = 0. Hvis fjørstivheten = 4 og massen til loddet er 1kg, så blir ω = 2. Grafisk vil x(t) ser då slik ut: (husk at vi reknar gradene i radianer)
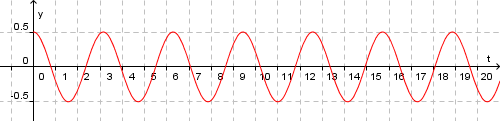
Her er amplituden A, lik 0.5. Utslaget x vil derfor variera mellom 0.5 og - 0.5. Dette kallast harmoniske svingningar.
Ein kan kanskje tru at når vi har vertikalt oppheng, så vil vi få ein annan løysing. For no vil jo tyngdekrafta også spela ein rolle.
Men det viser seg at sidan G er ei konstant kraft, så får vi ingen endring i den generelle løysinga på difflikninga. Den einaste forskjellen er at likevektspunktet blir flytta eit stykke nedover i forhold til der det ville vore uten påvirkning frå G.
Men når vi introduserer friksjon eller demping i systemet vårt, så kan løysinga på likninga bli slik, dersom dempinga er svak:
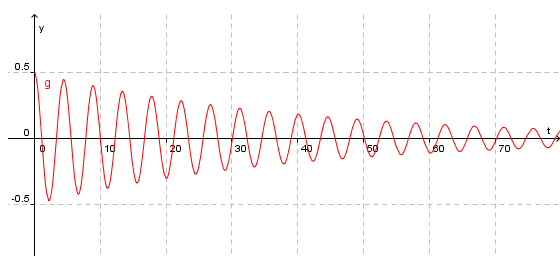
Her ser vi at amplituden A minkar mot null etter som tida går. Også frekvensen vil bli litt mindre i dette tilfellet. Dersom dempinga er sterkare vil ikkje pendelen rekka å svinga ein heil svingning før den blir dempa til null.
Hvis vi påvirkar eit svingesystem med eit ytre kraft som også svingar, så kan vi studera to fenomen som kallast beats og resonans. Eit eksempel kan vera at vi held ein fjørpendel og svingar handa opp og ned. Den frekvensen vi svingar handa med kallast den påtrykte frekvensen.
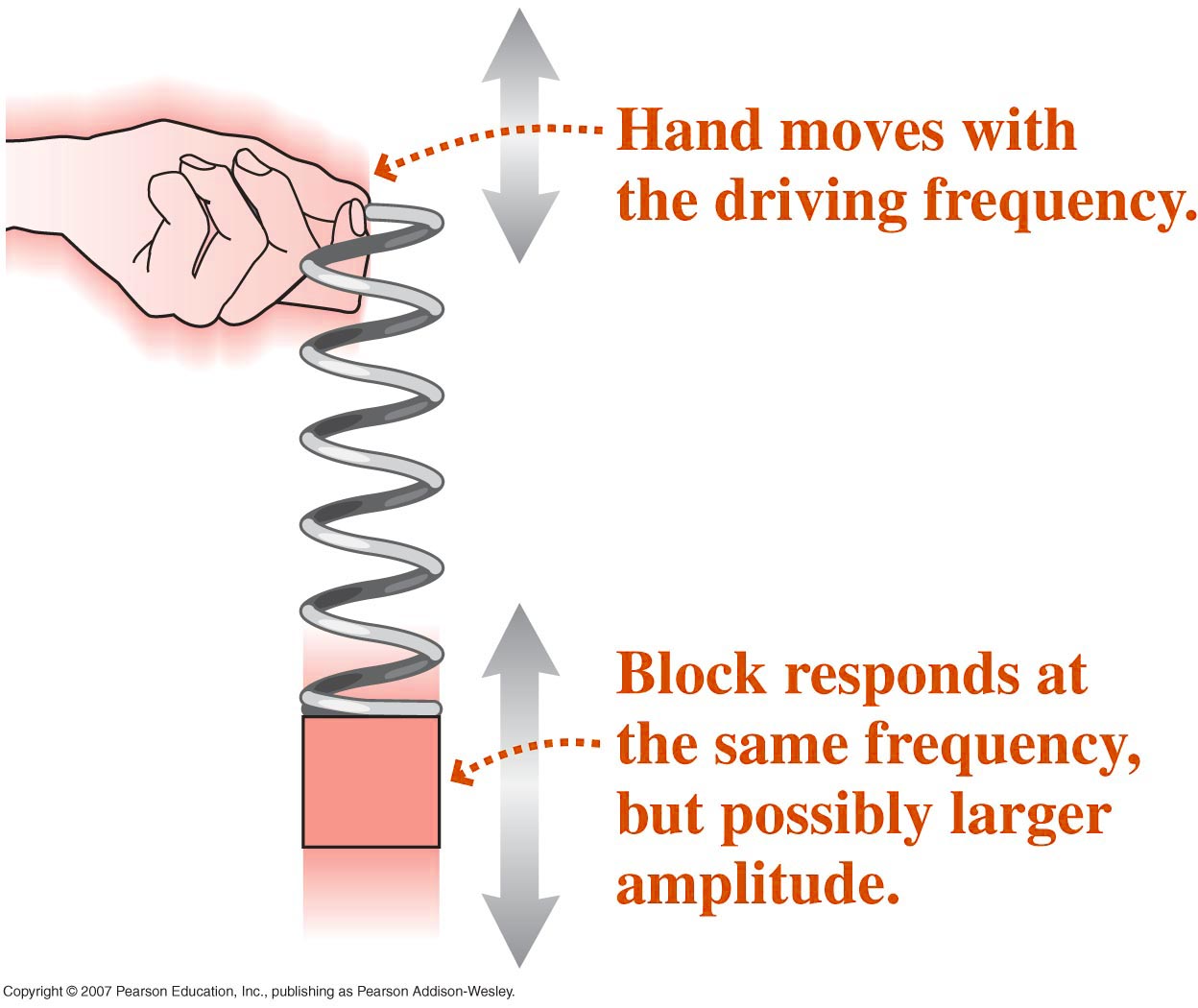
Hvis pendelen er udempa vil den svinga med den påtrykte frekvensen, men amplituden vil variera perdiodisk. Dette kallast beats. (Øverste figur). Sjå også simulering av beats. Hvis den derimot er dempa vil svingningane setta seg i ein steady-state, dvs at amplituden er konstant. (Nederste figur)
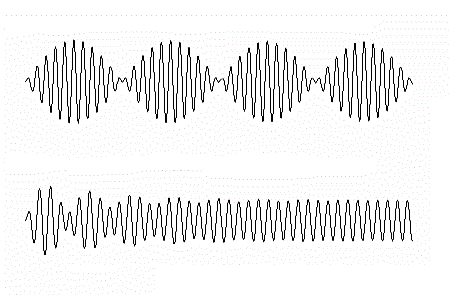
Når vi har situasjon to, dvs med demping, så kan vi også variera den påtrykte frekvensen f, dvs kor for hånda svingar. Når vi plottar amplituden i steday-state, som funksjon av frekvensen, så får vi noko som liknar på dette:
Når hånda svingar med ein frekvens langt frå systemet sin egenfrekvens (f0) så vil amplituden vera lav. Men når vi nærmar oss f0, så vil amplituden auka, og akkurat når f = f0. kan den bli veldig stor. Dette fenomenet kallast resonans. Kor høg amplituden bli, avheng av kor sterk demping vi har i systemet. For svakt dempa system kan amplituden bli så stor at heile systemet kollapsar.
Eit anna enkelt svingesystem er planpendelen. Dette er rett og slett eit lodd som heng i ein (ikkje-elastisk) tråd, eller (for store vinklar) ei stiv masselaus stang. Denne vil svinga omkring likevektspunktet, som er rett ned. Vi måler utslaget som ein vinkel θ mellom tråden og loddlinja. Krafta som trekkjer loddet inn mot senterlinja er ikkje proporsjonal med utslaget, men med sinus til utslaget. Dette ser vi ved å dekomponera tyngdekraften i ei kraft som virkar langs snora, dvs mg*cos θ, og ei som virkar normalt på snora, dvs mg*sin θ. Vi har ingen bevegelse i parllelt med snora, så den første komponenten er lik, men motsatt retta av snorkrafta som her er kalt T. Summen av kreftene på loddet er dermed lik mg*cos θ.
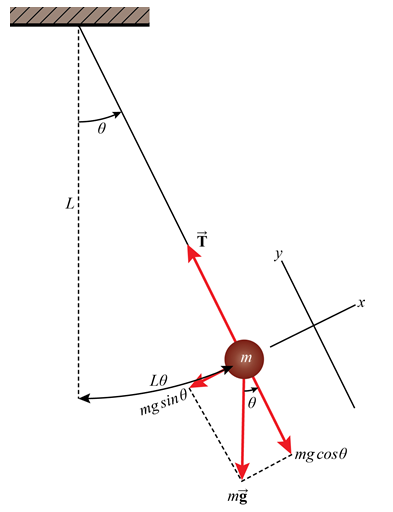
Det kan visast (Sjå feks Wikipedia) at differensial-likninga for ein planpendel uten demping blir:
Som vi ser, er den nesten heil lik likninga for den elastiske pendelen over. Og når vi reknar i radianer kan vi for små vinklar setja at sin θ er tilnærma lik θ. Då blir likningane heilt like i form (sjøl om vi har brukt andre navn på størrelsane), og vi får dermed den same oppførselen som ein elastisk pendel gir. Det vil sei at for små vinklar så får vi harmoniske svingningar, og vi kan få resonans osv. Men når vinkelen er større, vil planpendelen oppføra seg forskjellig frå den elastiske pendelen. Hvis vi drar loddet nesten heilt opp før vi slepp det, så ser kurven slik ut: (utslag i radianer)
Her er den tynne linja ein harmonisk svingning (dvs. ein cosinus-funksjon) mens den tjukke linja viser planpendelen.
Det viser seg at ein dempa planpendel med ei periodisk påtrykt ytre kraft kan fremvisa kaotiske svingningar. Dette skjer bare når parameterane er innanfor visse bestemte område. Du kan testa ein JavaScript-versjon av dette her. Men ein meir spektakulær utgave av ein kaotisk pendel er dobbelpendelen:

Applications of vibration models.