Simulering med pygame 5¶
Bevegelse i gravitasjonsfeltet¶
No skal vi laga ein simulering av ei leikeplanet i eit leikeunivers som går i bane rundt ei leikesol. Dette betyr at vi ikkje bruker realistiske verdiar for massar og avstandar. I tillegg set vi gravitasjonskonstanten G = 1. Dessuten gjer vi ein forenkling og seier at "sola" står heilt i ro. For at det skal stemma, så må vi anta at massen til "planeten" er mykje mindre enn "sola". I det verkelege solsystemet er sola 333 000 gonger tyngre enn jorda, og det betyr at feilen vi gjer ikkje er veldig stor.
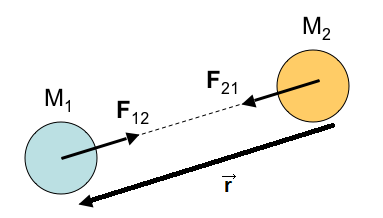
Hvis du har gått gjennom dei andre leksjonanene om pygame, så er strukturen i programma veldig like. Det nye her er korleis vi finn krafta som virkar på vår kule. Vi lar "sola" vera objekt 1, og "planeten" objekt 2. Figuren viser at krafta på "planeten" (F21) er i same retning som vektoren frå M2 til M1, som vi bare kallar →r
Gravitasjonsloven på vektorform kan skrivast:
→F=Gm1m2r2ˆr, der ˆr er ein enhetsvektor (som har lengde 1) som peikar i same retning som →r.
Det betyr at vi kan skriva at ˆr=→rr, og dermed kan vi skriva om likningen som:
→F=Gm1m2r3→r
På komponentform får vi då to likningar (når vi simulerer i 2D):
1) Fx=Gm1m2r3rx
2) Fy=Gm1m2r3ry
Før vi reknar ut krafta på "planeten" vår gir vi startverdiar for massar, posisjon og startfarten. Vi plasserer "sola" vår i punktet (200,200) og "planeten i punktet (150,200).
import math
G = 1 # Den gravitasjonelle konstanten
M1 = 2 # "Solmassen"
M2 = 0.001 # "Planetmassen"
x1 = 200 # x-verdi for "sola"
y1 = 200 # y-verdi for "sola" (Midt på)
x2 = 150 # x-verdi for "planeten"
y2 = y1 # y-verdi for "planeten"
vx = 0 # Startfart i x-retning
vy = 0.273 # Startfart i y-retning
No kan vi rekna ut x- og y-komponentane til krafta som virkar frå "sola" på "planeten" vår:
# r-vektor går frå objekt2 ("planeten") til objekt 1 ("sola")
rx = x1 - x2
ry = y1 - y2
r2 = (rx)**2 + (ry)**2 # Kvadratet av avstanden
r = math.sqrt(r2) # Avstanden
r3 = r*r*r
# Finn kraftkomponentane på objekt 2 ("planeten")
fx = G*M1*M2/r3*rx # Likning 1)
fy = G*M1*M2/r3*ry # Likning 2)
Når vi no har funne fx og fy, så kan vi dividera med massen til objekt 2 for å finna akselerasjonen i x- og y-retning:
ax = fx/M2
ay = fy/M2
Legg merke til at for denne utrekninga, så kunne vi ha latt vera å ta med M2 i det heile, og rekna ut akselerasjonen direkte. Slik vil vi gjera når vi skal rekna ut jordbanen seinare:
ax = G*M1/r3*rx
ay = G*M1/r3*ry
No kan vi rekna ut fart og posisjon omtrent på same måte som vi har gjort med sprettballen og svingningar:
# Finn farten i x- og y-retning
vx += ax
vy += ay
#Finn ny posisjon (x- og y-koordinater)
x2 += vx
y2 += vy
Denne koden er "motoren" i vårt program. Den utfører alle utrekningane vi treng for å simulera ein planetbane. Det som gjenstår er å putta den inn i ei løkke der vi tegnar "sola" og "planenet" for kvar iterasjon.
import pygame
import math
pygame.init()
BREDDE = 1000 # Bredden på vinduet
HOYDE = 400 # Høyden på vinduet
SOLRADIUS = 10
JORDRADIUS = 4
KOLLDIST = SOLRADIUS + JORDRADIUS
G = 1
M1 = 2
M2 = 0.001
JORD = (155, 255, 200)
SOL = (255,255,0)
HIMMEL = (0,0,100)
FPS = 200 #Frames Per Second, dvs kor fort animasjonen skal gå.
vindu = pygame.display.set_mode((BREDDE, HOYDE))
pygame.display.set_caption("Planetbane: ")
clock = pygame.time.Clock()
def game_loop():
x1 = 200 # x-verdi for "sola"
y1 = 200 # y-verdi for "sola"
x2 = 150 # x-verdi for "planeten"
y2 = y1 # y-verdi for "planeten"
vx = 0 # Startfart i x-retning
vy = 0.273 # Startfart i y-retning
running = True
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
return pygame.quit()
# r-vektor går frå objekt2 ("planeten") til objekt 1 ("sola")
rx = x1 - x2
ry = y1 - y2
r2 = (rx)**2 + (ry)**2 # Kvadratet av avstanden
r = math.sqrt(r2) # Avstanden
r3 = r*r*r
# Finn kraftkomponentane på objekt 2 ("planeten")
fx = G*M1*M2/r3*rx
fy = G*M1*M2/r3*ry
# Finn akselerasjonen i x- og y-retning
ax = fx/M2
ay = fy/M2
# Finn farten i x- og y-retning
vx += ax
vy += ay
#Finn ny posisjon (x- og y-koordinater)
x2 += vx
y2 += vy
# Tegnar systemet
vindu.fill(HIMMEL)
pygame.draw.circle(vindu, SOL, (int(x1), int(y1)), SOLRADIUS, 0)
pygame.draw.circle(vindu, JORD, (int(x2), int(y2)), JORDRADIUS, 0)
pygame.display.update()
#clock.tick(FPS)
game_loop()