Skrått kast med luftmotstand¶

Vi skal no simulera eit såkalt skrått kast med pygame, der vi tar hensyn til luftmotstanden. Då må vi først sjå litt på kreftene på ballen (eller det vi kastar) etter at vi har kasta den.

Figuren under viser dei viktigaste kreftene på ein ball i flukt: Det er G (tyngdekrafta), L (luftmotstanden), og det vi kan kalla for skrukrafta. Tyngdekrafta virkar rett nedover, og L virkar motsatt av bevegelsesretningen, dvs. motsatt av fartsvektorern v. Skrukrafta er eit resultat av Magnuseffekten, som fortel oss at ein ball som roterer (skrur / har spinn) opplever ei kraft som står normalt på rotasjonsaksen. Dette har alle som har spelt tennis, bordtennis eller fotball ha opplevt. Gir du ein ball topspin vil denne krafta virka nedover, Gir du backspin vil den virka oppover og hvis du gir med sideskru vil den virka sidelengs. For utrekninga nedanfor kjem vi til å anta at ballen, eller objektet vårt ikkje har skru, slik at vi kan sjå bort frå denne krafta. Ei anna kraft som ikkje er tegna inn på figuren, er oppdriften. Men i luft er oppdriften så liten at vi ser bort frå den også!

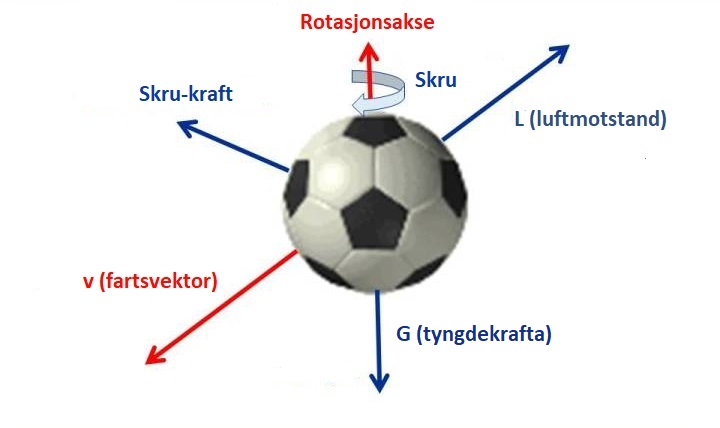
Tyngdekrafta, G, har vi alt vore borte i. I tyngdefeltet nær jorda, så kan vi setta den $\vec G = m \vec g$ , der m er massen til objektet (ballen), og g er lik 9.81 m/s2. Retningen er, som sagt, rett nedover, dvs. i positiv y-retning når vi bruker pygame.

Luftmotstanden er som regel modellert som proporsjonal med kvadratet av farten, dvs som $L = k v^2$ . Retningen er altså motsatt av fartsvektoren $\vec v$ . Vi skal no summera kreftene. Det vil sei at vi skal finna $\vec F = \vec G + \vec L$ . Det betyr at vi må finna komponentane $F_x = G_x + L_x$ og $F_y = G_y + L_y$ . Sidan G virkar rett nedover, blir x-komponenten lik 0, og y-komponenten lik mg, dvs at vi har

$F_x = L_x$ og $F_y = mg + L_y$ .

For å finna komponentane til L, så ser vi først på ein figur til:

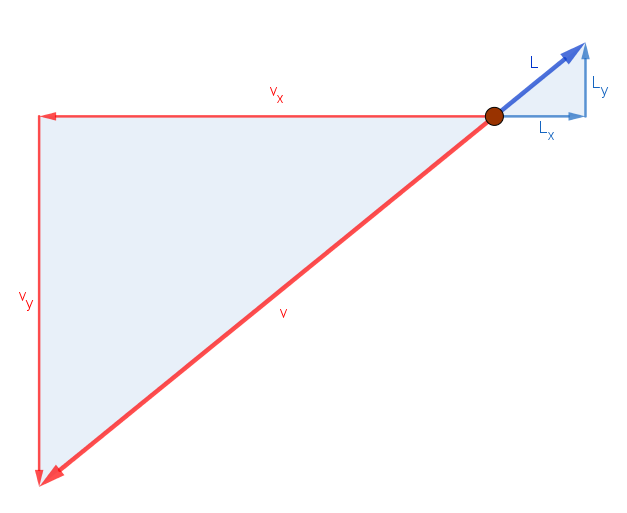
Vi ser på ein snapshot av ein ball på vei nedover til venstre. Den store trekanten til venstre viser då vektorane (uten vektorsymbol) v, med sine komponentar vx og vy, og den lille trekanten viser luftmotstanden L, med sine komponentar Lx og Ly. Sidan v og L er parallelle men motsatt retta vil disse to trekantane vera likeforma. Då kan vi setja opp følgande likning: $\frac{L_x}{v_x} = \frac{L}{v}$ . Når vi multipliserer med vx på begge sider får vi då:

$L_x = L \frac{v_x}{v}$

Tilsvarande finn vi for y-komponenten:

$L_y = L \frac{v_y}{v}$

Til sist set vi inn at $L = kv^2$ i formlane og får:

$L_x = kv^2 \frac{v_x}{v} = kv v_x$ , og for y: $L_y = kv v_y$

Då er det på tide å laga programmet vårt. Så vi definerer først noken konstantar. Sidan vi her bruker spillkoordinater, set vi bare verdiar som ikkje har fysisk betydning. Vi gir også startverdiar for posisjonen (x,y) og fartsvektoren (vx,vy):

M = 1           # Masse
g = 0.1         # Tyngdeakselerasjonen
G = M*g         # Tyngdekraften (konstant)
k = 0.001       # Konstanten for luftmotstand
    
x = 10          # startverdi for x
y = 150         # Startverdi for y
vx = 5          # Startfart i x-retning
vy = -5         # Startfart i y-retning

No har vi dei verdiane vi treng for å finna farten og luftmotstanden. Merk minustegnet for Lx og Ly, som fortel at L er motsatt retta v:

import math

v = math.sqrt(vx**2 + vy**2) # Farten    

Lx = -k*v*vx                 # x-komponenten av L
Ly = -k*v*vy                 # x-komponenten av L

Deretter kan vi finna hhv. Fx, Fy og deretter ax, ay:

Fx = Lx
Fy = G + Ly
        
ax = Fx / M
ay = Fy / M

Til slutt kan vi så finna farten (vx,vy) og den nye posisjonen (x,y)

vx += ax
vy += ay

x += vx 
y += vy

For å laga ein animasjon må vi no laga ei løkke der vi oppdaterer luftmotstanden, Summen av kreftene (F), akselerasjonen a og fart og posisjon i denne rekkefølgen. Vi må også tegna ballen vår. Heil programmet ser dermed slik ut:

import pygame, math

pygame.init() # Startar pygame

BREDDE = 800 # Bredden på vinduet
HOYDE = 600 # Høyden på vinduet

# Definerer RGB-fargar
BAKGRUNN =  (100, 200, 255)
BALL = (255, 80, 0)

FPS = 20 #Frames Per Second, dvs kor fort animasjonen skal gå.

vindu = pygame.display.set_mode((BREDDE, HOYDE)) # Definerer vindu / overflate
pygame.display.set_caption("Sprettball: ") # Overskrift for vinduet
clock = pygame.time.Clock()

def game_loop():
    
    RADIUS = 2      # Radius
    M = 1           # Masse
    g = 0.1         # Tyngdeakselerasjonen
    G = M*g         # Tyngdekraften (konstant)
    k = 0.001       # Konstanten for luftmotstand
    
    x = 10          # startverdi for x
    y = 150         # Startverdi for y
    vx = 5          # Startfart i x-retning
    vy = -5         # Startfart i y-retning

    running = True # Boolsk variabel. Løkka vil løpa så lenge denne er SANN
    stop = False # Om animasjonen skal gå eller ikkje
    while running:
        
        # Lukker vindu og stoppar programmet:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                return pygame.quit() 
            
        v = math.sqrt(vx**2 + vy**2) # Farten    

        Lx = -k*v*vx                 # x-komponenten av L
        Ly = -k*v*vy                 # x-komponenten av L
        
        Fx = Lx
        Fy = G + Ly
        
        ax = Fx / M
        ay = Fy / M
       
        # Hvis kollisjon med venstre eller høgre kant, stoppar vi animasjonen
        if x + RADIUS > BREDDE or x < RADIUS:
            stop = True
        # Hvis kollisjon med øvre eller nedre kant, stoppar vi animasjonen
        if y + vy + RADIUS > HOYDE or y + vy < RADIUS:
            stop = True
        else:
            vx += ax
            vy += ay
            
        if not stop:
            x += vx # Oppdaterer x-koordinat
            y += vy # Oppdaterer y-koordinat

        # Tegnar vindu og ball
        #vindu.fill(BAKGRUNN) # Fyller vindu med ein farge
        pygame.draw.circle(vindu, BALL, (int(x), int(y)), RADIUS, 0)
        pygame.display.update()
        clock.tick(FPS)

game_loop()

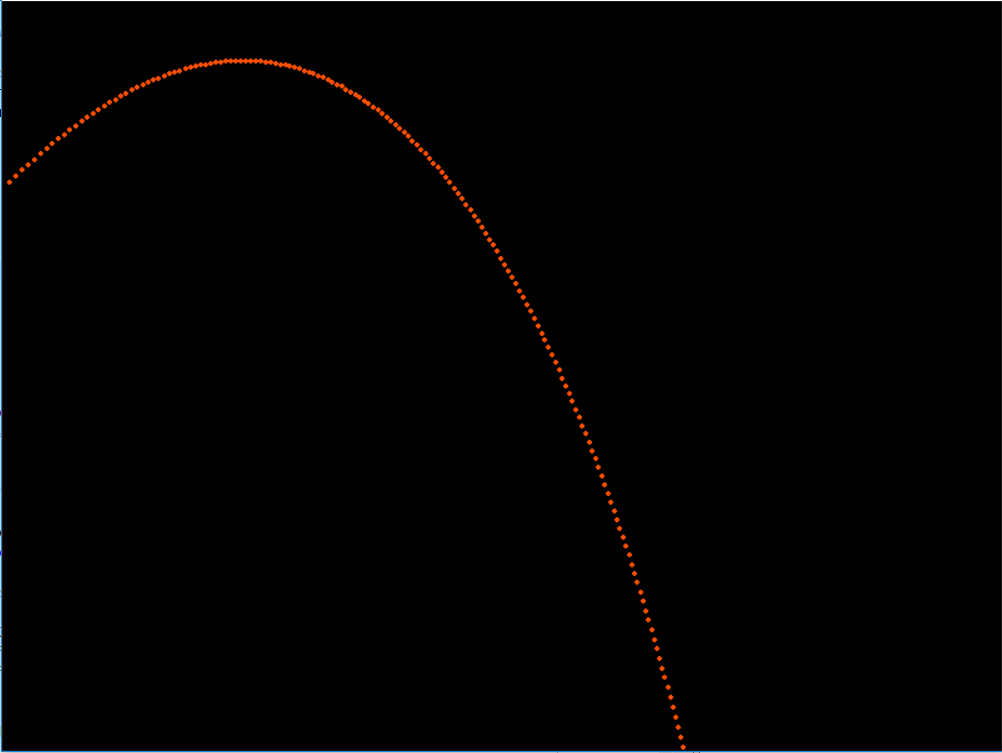
Merk at koden som tegnar bakgrunnen her er kommentert bort, og at vi har ganske lav FPS. Det medfører at alle posisjonane til ballen blir tegna i same vindu. Resultatet er slik:

Oppgaver¶

1) Gitt k = 0,008, og $v_x = 20$ og $x_y = 15$ . Finn først $v^2$ og v, og finn deretter L, $L_x$ og $L_y$ . Vis at vektorane v og L er parallelle, men motsatt retta, og vis også at $L = kv^2$ .

2) I koden over er k satt lik 0.001. Varier verdien og sjå korleis fallkurven endrar seg. Korleis ser kurven ut hvis vi ser k = 0?

3) Sjå Graftegning med Matplotlib, og prøv å laga ein graf der du plottar kurvene for ulike k-verdiar, inklusivt k = 0, i same diagrammet.

4) I programmet vårt har vi brukt utgangsfarten (5,-5) og tyngdeakselerasjonen a = 0.001. Bruk det du kan om bevegelseslikningane for konstant akselerasjon, og vektorfunksjonar og tegn kurven for denne bevegelsen. Samanlikn denne kurven med kurven vi fekk for tilfellet k = 0. Tegn gjerne i same diagrammet og / eller finn differansen mellom y-verdiar for same x-verdi. Korleis passar det?