Smittespredning

Her skal vi sjå på ein del måtar å simulera spredning av sjukdomar gjennom ein befolkning. Alle disse er såkalte kompartement-modellar (compartment models på engelsk), der vi kan tegna boksar for å illustrera modellen. I disse modellane tenkjer vi oss individ gruppert etter kva tilstand dei er i. Kvar kategori blir derfor ein slags delpopulasjon, og vi får ein differsiallikning for kvar kategori.

SEIR-modellen

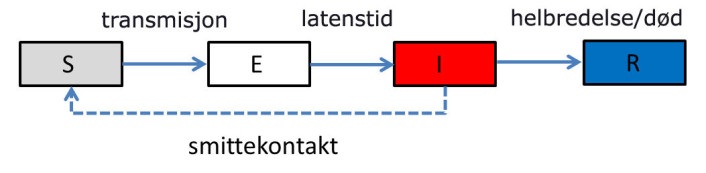
Vi skal sjå på ulike modellar, men alle er egentlig er ein variantar av den same. Derfor ser vi først på SEIR-modellen som har fire kategoriar:

• S står for  Susceptible. Det er antal personar som er mottakelige for smitte, dvs dei som ikkje er blitt vaksinert eller immune etter å ha vore sjuke.
• E står for  Eksponert. Det er antal personar som har blitt smitta, men er ikkje sjuk og kan ikkje smitta andre. Noken gonger brukes L for Latent.
• I står for Infiserte. Det er antal personar som har blitt sjuke, og som kan smitta andre. Det tar ei tid før sjukdommen bryt ut, og dette kallast latenstid.
• R står for Recovered (Noken seier Removed). Det er antal personar som enten er friske eller døde. Uansett kan dei i denne modellen ikkje lenger smitta andre.

Kvar kategori er representert ved ein boks, eit såkalla compartment / kompartement. Så boksen S "inneheld" alle individ som er smittbare. Når dei blir smitta "flyttar" dei over i boks E, deretter vil dei (før eller seinare) gå over i I-boksen, og til sist til R boksen. I denne modellen vil derfor alle som regel til slutt havna i boks R. Det fins unntak som vi skal diskutera nedanfor. Dermed kan vi visualisera modellen på denne måten:

Differensiallilkningane

Utfordringen blir no å finna ut kor fort flyten går mellom dei ulike boksane, og korleis den varierer. Då kan vi finna endringen i ein boks per tid ved å rekna flyten inn i boksen minus ut av boksen. Og som figuren viser: boks S har bare flyt ut, og boks R har bare inn. Likningane for disse inneheld derfor bare eit ledd. Dei to andre har både flyt inn og ut, og har derfor to ledd. Endringen per tid i ein boks er det same som den deriverte av antalet i boksen. Husk at S, E, I og R er funksjonar av tida, altså skulle vi egentlig skrive S(t) osv. Den deriverte av S(t) skriv vi vanligvis for S'(t), men her bruker vi ein annan notasjon (den såkalte Leibniz-notasjonen) og skriv dS/dt. Dermed har vi dei fire  differensiallikningane:

Forklaring

• S: Endringen i boks S per tid er lik antallet nysmitta per tid. For å bli smitta må ein komma i kontakt med ein frå I-boksen. Hvis alle i populasjonen har same sannsynlighet for å møta alle andre, så kan vi sei at sannsynligheten for å bli smitta er proporsjonal med andelen smitta, altså β*I/N, der β er ein konstant. For å få det totale antalet nysmitta må vi ganga med antalet i S-boksen. Dermed blir flyten ut av S-boksen lik -βSI/N. Minustegnet kjem altså fordi det er flyt ut.
• E: Det same leddet finn vi for boks E (i linje to), bare med positivt fortegn: βSI/N. Dette er flyten inn. Flyten ut er proporsjonal med antalet i boksen, dvs. E. Det vil sei at ein viss andel av E-folket vil komma over i boks I per tid, og denne andelen er gitt ved konstanten σ. Flyten ut er altså -σE. 
• I: Når vi då ser på boks I, finn vi her også igjen dette leddet med positivt fortegn: σE. Dette er  flyten inn. Flyten ut er også her proporsjonal med antalet i boksen, dvs. I. Men her med ein annan konstant. Så vi får; -γI.
• R: Her er det bare flyt inn, og den er lik flyt ut av I, men med positivt fortegn, altså γI.

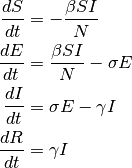
Her har vi fire differensiallikningar, der kvar linje gir oss eit uttrykk for den deriverte av antallet i den aktuelle boksen. Likning ein gir oss likninga for S'. Då kan vi finna endringen i løpet av ein kort tidsperiode dt, som S' * dt. Den nye verdien for S blir då S + S' * dt. Vi gjer akkurat det same for variablane E, I og R. Så algoritmen vi skal bruka er å først finna dei deriverte av alle variablane S, E, I og R ved hjelp av formlane. Deretter oppdaterer vi disse variablane. Når vi gjer dette i ei løkker, der vi suksessivt oppdaterer S, E, I og R kan vi simulera korleis sjukdomen vil forplanta seg gjennom populasjonen. Dei tre parameterane β, σ og γ bestemmer kor fort flyten kan gå mellom dei ulike boksane.

Hvis vi summerer alle ledda på høgre side av differensiallikningane over, ser vi at summen blir 0. Det er som forventa, sidan modellen vår ikkje tar høgde for at det totale antalet folk, som vi kan kalla N, endrar seg, dei bare "flyttar" seg mellom dei ulike boksane. Noken modellar tar med ein boks for døde (D), men dette tel med, slik at også her blir N konstant.

Det vi har skissert her, er den såkalte Eulermetoden. Med denne kan vi løysa likningssettet numerisk. For å gjera det treng vi å vita verdiane til dei tre parameterane, og vi treng å vita startverdiane for S, E, I og R. Hvis vi kallar det totale antalet mennesker i modellen som N.  i vil vi normalt setja startverdiane slik at I er 1, og S er resten, dvs. N - 1. Dvs. at E = 0 og R = 0. 

Simuleringar

Her er eksempel på korleis dette kan sjå ut vi kjører modellen i 100 "dagar", når N = 1000:

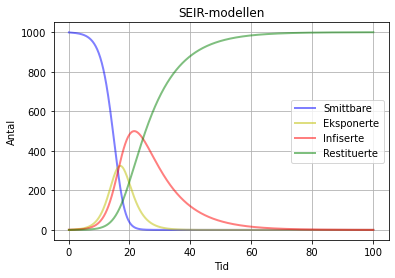
SEIR-modell med beta = 1.3 , sigma = 0.3 og gamma = 0.1. Her ser vi at heile populasjonen (alle 1000) er resitituerte, dvs. friske.

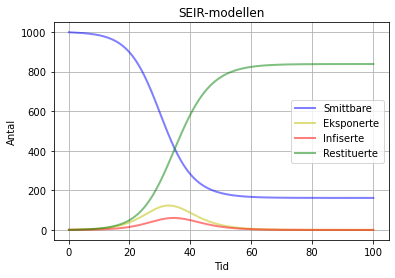
SEIR-modell med beta = 1.3 , sigma = 0.3 og gamma = 0.6. Den einaste forskjellen her, er at gamma er sett til 0.6. Resultatet er at 838 er restituerte, mens dei resterande 162 fremdeles smittbare. Men dei vil aldri bli smitta fordi både E og I har gått ned til 0. Det som skjer her er at det er stor flyt ut av I-boksen slik at den blir tømt veldig fort. Dermed er det ingen igjen som kan smitta andre.

Tolking av parameterane

• Parameteren som vi endra på over, altså gamma, fortel nåke om kor lang tid det tar før ein infisert blir frisk, altså restitusjonstida. Vi kan rekna at restitusjonstida er 1/gamma. Det vil sei at i siste kjøring er den under 2 dagar, mens i den første er den ti dagar.
• Beta svarar til smittsomhetsgraden. Jo større verdi, jo lettare / fortare blir folk smitta.
• Sigma svarar fortel om inkubasjonstida. Vi kan rekna den som 1/sigma.

Variantar av SEIR:

Avhengig av korleis sjukdommen vi studerer, artar seg, kan vi konstruera ulike variantar av SEIR-modellen. Vi kan for eksempel leggja til ein boks til slutt.

SEIRD-modellen

Denne varianten er lik SEIR bortsett frå at vi har to mulige utgangar, nemlig at ein blir restituert, eller at ein dør. Så det er ein ekstra boks D, og ein ny parameter μ som styrer flyten til kor mange av dei Infiserte som dør. Modellen ser slik ut:

Simulering

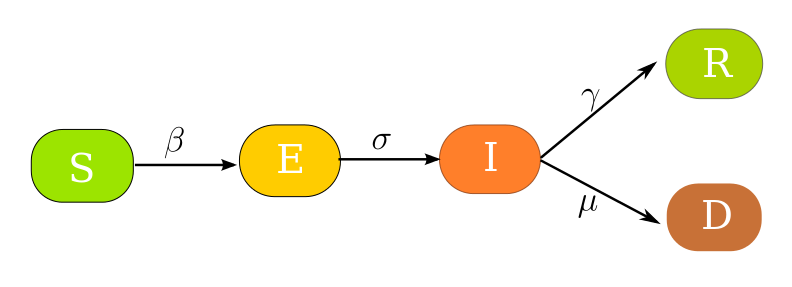
Her har vi kjørt slik at gamma + mu er lik 0.1, dvs. det gamma var i den øverste SEIR-kjøringa:

SEIRD-modell med beta = 1.3 , sigma = 0.3 gamma = 0.06 og mu = 0.04. Her ser vi at S, E og I oppfører seg akkurat slik som i den første kjøringa, men i staden for at alle blir restituerte så får vi R = 600, og D = 400. Men det gir jo 1000 til saman. Hvis vi set gamma = 0.4 og mu = 0.2, dvs tilsaman 0.6, så får vi ein graf som liknar meir på den andre SEIR-kjøringa over, dvs, med same antal smittbare (162) mens det vi hadde for R (838), no blir fordelt på R (559) og D (279). Alt i alt ikkje så spennande for oss som simulerer, men desto meir spennande for dei som er infiserte!

SEIRS-modellen

SEIR-modellen  forutset at alle som har hatt sjukdommen blir immune. Slik er det jo ikkje alltid i verkeligheten. For mange sjukdommar forsvinn immuniteten etter ei stund. For å modellera dette må vil tillata ein flyt tilbake til S-boksen. Då ser modellen slik ut:

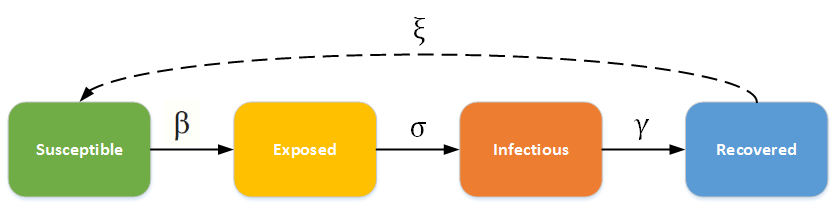
Her er det altså ingen ny boks, men det er ein flyt tilbake frå R-boksen til S-boksen. Flyten her, er bestemt av parameteren ξ (ksi).

Simulering

Hvis vi set ksi = 0 her, så får vi tilbake SEIR-modellen. Det er ikkje så interessant, men er greit å prøva for å sjå om programmet virkar. Ellers kan ei kjøring sjå slik ut:

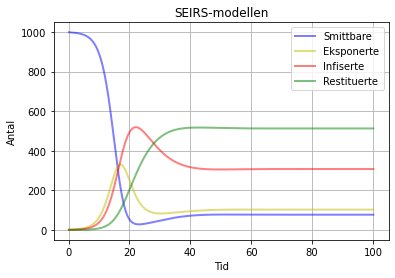
SEIRS-modell med beta = 1.3 , sigma = 0.3 gamma = 0.1 og ksi = 0.06. No skjer det at ingen av boksane blir tomme, men alle stabiliserer seg på ein fast verdi. Dette betyr at sjukdomen aldri forsvinn frå populasjonen, men at folk smitta igjentatte gonger.

Andre variantar

Forenklingar

Hvis vi kuttar ut ein eller fleire boksar med tilhøyrande koblingar, så kan vi for eksempel få SIR- og SIRS-modellar. Her er det ingen inkubasjonstid. Det betyr at folk som blir smitta, kan smitta andre med ein gong. Hvis vi kuttar ut også R-boksen kan vi då få SI- og SIS-modellar. Men disse vil ellers ikkje oppføra seg veldig forskjellig frå dei vi alt har sett på, og vi skal ikkje gå nærmare inn på dei. Men du kan lesa meir om dei i lenkene under.

Vidareutvikling

Men motsatt er det mange grep vi kan gjera for å gjera modellane våre meir komplekse for å prøva å etterlikna verkelige sjukdommar. Vi kan innføra forsinkelsar, vi kan ha parameterar som varierer med tida (for eksempel årsvariasjonar), og vi kan innføra såkalt vital dynamikk.  Det betyr bare at vi i tillegg til å modellera sjukdommen, også modellerer fødsel og (naturlig) død. Då vil vi kunna sjå at sjukdommane går i bølger, slik som det ofte skjer i verkeligheten. Ein annan mulighet er å la populasjonen "leva" i eit nettverk. Det vil sei at ikkje alle har like stor sannsynlighet for å smitta kvarandre. Slik er det jo opplagt i verkeligheten: vi treff  jo oftast dei same personane: familie, venner, kollegaer på jobb, eller klassevenner. Dette påvirkar korleis sjukdommen artar seg. Ein kan tenkja seg at ulike aldersgrupper har ulike verdiar for parameterane, fordi sjukdomar artar seg jo ikkje likt for barn som for vaksne / eldre. Ein annan mulighet er å studera korleis ein kan styra epidemiar ved feks. å vaksinera, eller ved å begrensa folk sine bevegelsar osv. Alt dette, og meir til, driv folk og forskar på for å få betre modellar som kan hjelpa oss å forstå, og bekjempa sjukdomar. 

Individbaserte modellar.

LENKER

Slik simuleres et virusutbrudd.

SEIR and SEIRS models

SIR and SIRS models.

SI and SIS models.

Mathematical modelling of infectious disease.

epydemic: Epidemic simulations on networks in Python.

Networks and epidemic models. omfattande

Spreading of diseases (ser passelig ut!)