Koffein er det virksomme stoffet i blant anna kaffi, cola, te, energidrikker og kakao. Ein vanlig kopp kaffi inneheld omtrent 150 milligram koffein avhengig av styrken. Ein original iskaffe, skal visstnok innehalda koffein tilsvarande ein espresso, ca 65 mg. Koffein er eit såkalt alkaloid med den kjemiske formelen C8H10N4O2. Det blir sagt at det gjennomsnitt bare tar omlag 45 minuttar før 99% av koffeinet i ein kopp blir absorbert.
Etter at koffeinet har kome over i blodet, blir det brote ned hovedsakelig i levera av spesielle ensymer. Så snart koffeinet kjem inn i blodstraumen begynner levera å bryta ned molekyla til andre stoff som på engelsk heiter theophylline, theobromine, og paraxanthine. Denne prosessen kallast eliminering.
Halveringstida for koffein hos mennesker, dvs den tida det tar før halvparten av stoffet er brote ned, kan vera frå 4 til 6 timar i gjennomsnitt, men det er store individuelle forskjellar. Både genetiske og andre faktorar (som røyking) vil påvirka kor fort koffeinet blir tatt opp i blodet, og kor fort det går ut igjen.

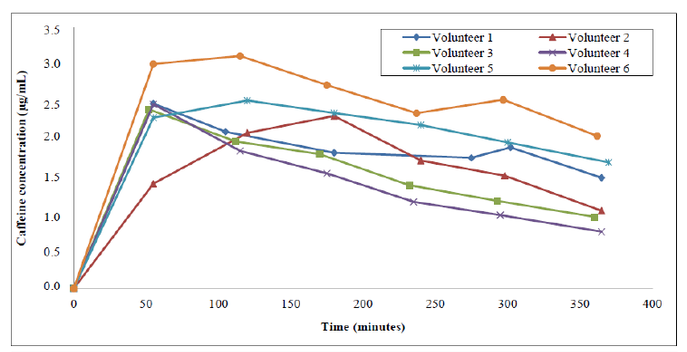
Figur 1: Figuren, som er henta herfrå. viser korleis koffeinkonsentrasjonen endrar seg for seks forsøkspersonar i løpet av dei første seks timane etter inntak. Enheten her er μg / mL, og det er det same som mg/L- (milligram per liter) som vi kjem til å bruka nedanfor. Vi ser at noken når toppen av kurven ganske fort (ca 50 min) mens for andre går det lenger tid. (over 100 min)
Her skal vi sjå korleis vi kan bruka ein såkalt kompartmentmodell for å finna ein funksjon for korleis konsentrasjonen i blodet utviklar seg over tid. Eit compartment kan vi oversetja til beholdar, og ein tenkjer seg då at kroppen er delt opp i ulike beholdarar som stoff kan flyta mellom. Dette er sjølsagt ein matematisk forenkling, for så enkelt er det ikkje i kroppen. Men det kan likevel gi gode estimat for ulike prosessar.
Avhengig av kva ein skal modellera, opererer ein med ein, to, tre og gjerne fleire beholdarar. I dette tilfellet skal vi bruka to: ein for magen og eit for blodet. Sjølsagt går stoffet også ut i resten av kroppen, men det ser vi ikkje på her. Sidan koffein begynner å gå over i blodet allerede mens det er i munnen, er beholdar 1 då egentlig både munnen, halsen, magen og tarmen. Men vi kallar det "magen" her. Vi får då følgande modell:
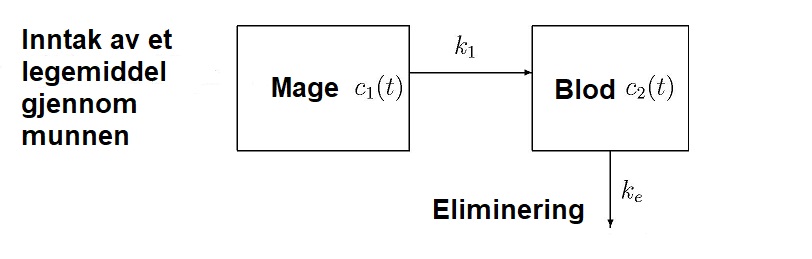
Figur 2: To-kompartment-modell for inntak av koffein.
I kvar beholdar tenkjer vi at det er ei viss konsentrasjon av koffein, som vi skriv c1(t) for magen, og c2(t) for blodet. Disse konsentrasjonane vil endra seg over tid ved at det flyt stoff inn og ut av beholdaren. Så vi har den enkle samanhengen for endringen i ein beholdar:
endring av konsentrasjon = flyt inn - flyt ut
No skal vi setja opp ein differensiallikning for kvar av behaldarane. Endringen av konsentrasjonen er lik den deriverte av c(t)-funksjonen, altså c'(t). Så antar vi at stoff-flyten ut av ein behaldar er proporsjonal med konsentrasjonen i denne behaldaren. Vi antar også at flyten inn i blodet er lik flyten ut av magen, Då kan vi setja opp følgande likningar for våre to behaldarar:
(1) c1'(t) = - k1 c1(t)
(2) c2'(t) = k1 c1(t) - ke
c2(t)
Likning (1) fortel at det er ingen flyt inn i magen. Vi tenkjer at koffeinet blir drukke, og ved t = 0, er alt stoffet allerede i magen, og begynner deretter å gå over i blodet. Flyten ut av beholdar 1 er proporsjonal med konsentrasjonen der, og k1 er då proporsjonalitetskonstanten. Denne fortel kor fort koffeinet forlet magen. Jo større tall, jo fortare går det.
Av figur 1 ser vi at flyten ut av magen er lik flyten inn i blodet. Så det forklarer første ledd i likning (2), som er det same som høgre side i (1), bare med positivt fortegn. Derfrå blir det eliminert av levera. Det går ut av blodet med fart definert av proporsjonalitetskonstanten ke ("e" for "exit"), og det forklarer ledd 2.
Likning 1 og 2 over, er differensiallikningar. Disse er eksakt løysbare, dvs. at vi kan finna dei ved rekning. Vi tar ikkje opp løysingsmetodar her, men det kan visast, som det heiter, at den generelle løysinga er:
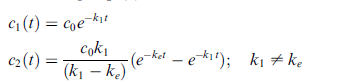
Her er c0 startverdien for konsentrasjonen i magen. Hvis du kan derivera disse funksjonane, er det ikkje vanskelig å visa at dei passar i likning (1) og (2).
For å finna funksjonane konkret må vi vita verdiane for konstantane c0,
k1 og ke. Vi lar* disse vera:
c0 = 12.32
k1 = 3.29
ke = 0.098
Med disse verdiane får vi følgande funksjonar:
c1(t) = 12.3 e-3.29t
c2(t) = 12.7 (e-0.098t - e-3.29t)
Då kan vi plotta disse, og sjå korleis konsentrasjonen av koffein utviklar seg i løpet av 24 timar:
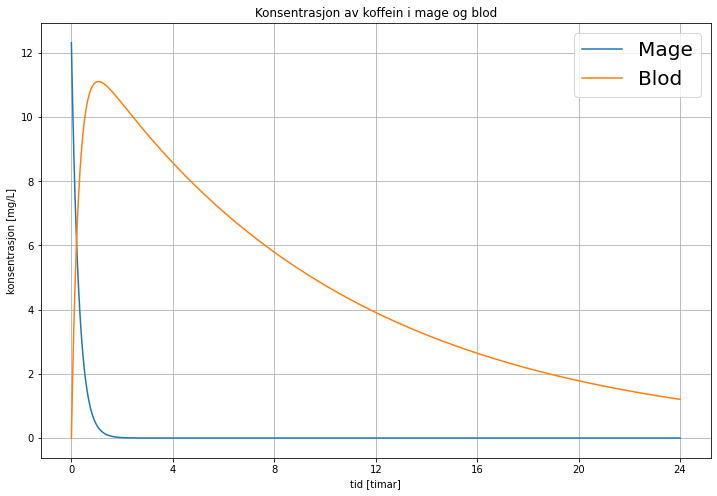
Figur 3: Plott av dei eksakte løysingane for c1(t) (blå kurve) og c2(t) (oransje). c2 har ein topp ved ca 65 min, og halveringstida er ca. 7 timar.
c1 blir ein vanlig eksponential-funksjon, og når eksponenten er negativ, får vi den karakteristiske "decay"-kurven (blå). I magen starter vi med konsentrasjonen 12.3 mg/L. Enheten er altså mg koffein per liter blod. Hvis vi antar at ein vaksen har omtrent 5l blod, så har vedkommande då tatt inn ca 62 mg koffein - altså omtrent det du får i ein standard iskaffi.
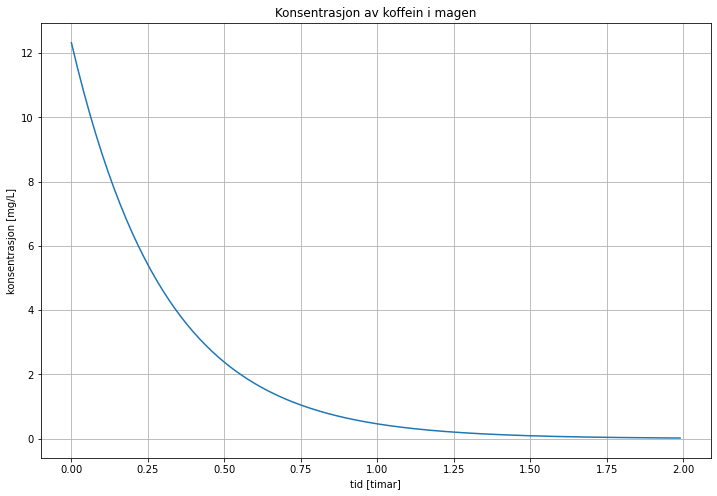
Figur 4: Plott av kun c1(t) Figuren viser korleis konsentrasjonen i magen dei første 2 timane. Mengden er halvert etter ca 13 min, og det er 1% igjen etter 1 time og 24 min. Dette er meir enn det som blir sitert (45 min) overalt på nett. Men når ein leitar etter faktiske grafar, så ser det ut til å vera innanfor. Sjå figur 1.
Men det er c2-funksjonen som er den mest interessante her. Det er ein samansett funksjon, og for å forstå ka som skjer her, er det greit å først diskutera korleis kurven ville sett ut hvis ikkje koffeinet vart eliminert av levera. Det svarar til å setja ke = 0. Det ville gitt den ein kurve som er opp-ned av c1-kurven, og vist som den blå kurven under. Konsentrasjonen aukar fort til maxverdi, og blir der.
Så kan vi sjå på ka som ville skjedd hvis vi bare injiserte koffeinet direkte i blodet (neppe ein god ide!). Då vil vi få ein liknande kurve som konsentrasjonen i magen, dvs ein vanlig eksponentialfunksjon, men den flatar mykje saktare ut enn c1-kurven. Denne er vist som grønt under.
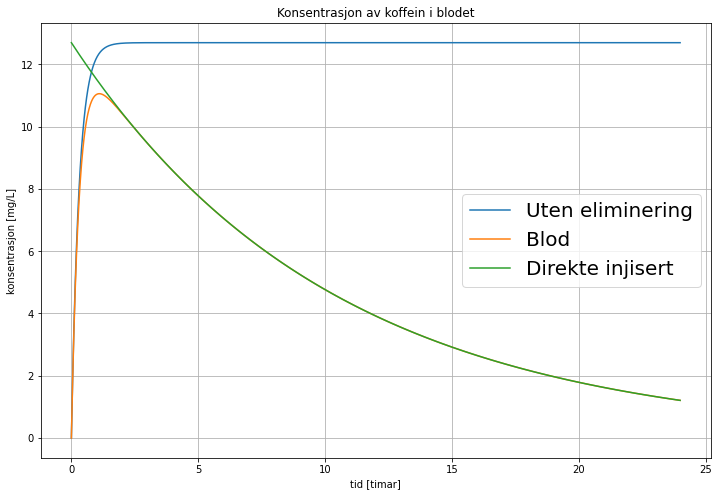
Figur 5: Figuren viser den egentlige kurven for c2 (oransje), kurve for direkte injeksjon (grøn) og kurve uten eliminering (blå). Vi ser tydelig at tidlig i forløpet, dvs fram til ca 25 minutter, så føljer c2-kurven den blå. Det er fordi det inntil då har vore så lite koffein i blodet at det ikkje har blitt eliminert særlig mykje frå blodet. Så ser vi at c2-kurven begynner å bøya av fordi det er såpass mykje koffein i blodet at merkbare mengder begynner å gå ut igjen. Og etter kort tid når c2 eit toppunkt (65 min), og begynner å gå ned. Deretter, etter ca 100 min, føljer c2 den den grøne kurven. Her er nesten alt koffein komt inn i blodet, og frå no av er det normalt "decay".
Moderne farmakologiske prinsipper for intravenøs anestesi.
Single and multiple compartment models of drug distribution
Chapter 4. Multicompartment Models: Intravenous Bolus Administration..
...